Spis treści

1 Temperatura Debye’a

1.1 Podstawy i wzory

Temperaturę Debye’a można obliczyć korzystając ze znajomości prędkości rozchodzenia się dźwięku w krysztale. Jeżeli potrafimy uśrednić tę wartość po wszystkich kierunkach kryształu, otrzymamy prędkość średnią v_m. Ponieważ jest ona złożeniem trzech niezależnych prędkości: podłużnej v_L oraz dwóch poprzecznych v_TA i v_TB, więc możemy ją obliczyć korzystając z zależności:

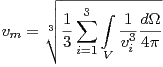(1)

Znając już wartość prędkości średniej, możemy obliczyć temperaturę Debye’a z niej wynikającą. Potrzebne nam będą jeszcze:

• gęstość kryształu ;
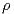• masa molowa M;
• ilość atomów w cząsteczce p (np. dla CaF₂, p = 3).

Temperatura Debye’a jest w takim wypadku określona wzorem (2):

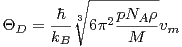(2)

1.2 Skrypt

Poniższy skrypt pozwala na szybkie wyliczenie temperatury Debye’a dla dowolnego kryształu.

2 Sprzężenie spin-fonon

2.1 Podstawy i wzory

W teorii elektronowej relaksacji spin-siatka pojawia się element macierzowy sprzężenia spin-fonon. Jest on również obecny w wielu innych teoriach opisujących różne zjawiska zachodzące w kryształach (jak choćby nadprzewodnictwo).
Proces relaksacji spin-siatka możemy opisać czasem charakterystycznym T₁. Na czas ten składa się szereg różnych procesów, jednak w kryształach najczęściej najbardziej dominującym procesem jest dwufononowy proces ramanowski, gdzie zależność czasu T₁ od temperatury dla jonów kramersowskich (z nieparzystą liczbą elektronów) opisany jest zależnością:

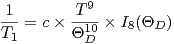(3)

gdzie _D jest temperaturą Debye’a, natomiast I₈ jest całką transportu obliczaną numerycznie.

Współczynnik c zależy od szeregu czynników, a rozpisanie go w jawnej postać prowadzi do równania:

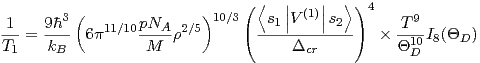(4)

Pojawiły się tutaj dwie nowe wielkości:

• energia wirtualnego poziomu krystalicznego _cr, przez który zachodzi relaksacja;
• element macierzowy spin-fonon .

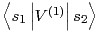Nie potrafimy wyliczyć teoretycznie tego elementu, lecz możemy podać jego wartość wynikającą z eksperymentu. Jest on przecież zawarty w równaniu (4). Jeżeli otrzymamy z eksperymentu elektronowej relaksacji spinowej wartość współczynnika c to będziemy mogli wyliczyć wartość tego elementu.

2.2 Skrypt

Poniższy skrypt oblicza wartość elementu macierzowego sprzężenia spin-fonon.