Research topics

Elastic properties of Hard Sphere systems with structural inclusions

The elastic properties of materials are among the earliest physical quantities studied by man. We currently have high-accuracy values for such material quantities as, among others, modulus of elasticity (C), Young's modulus (Y), bulk modulus (B), shear modulus (μ), or Poisson's ratio (ν). However, the relationships between these macroscopic elastic properties and the microscopic structure of materials and the phenomena occurring at the level of this structure are not fully explored and understood. A clear example of this is the fact that less than 40 years ago, in textbooks dealing with the elasticity of matter, one could find records that materials characterized by a negative Poisson's ratio (NPR) were not known. They were proposed and produced only in the second half of the 1980s. Today, when the challenges faced by engineers in virtually all fields require the creation of new materials, often with very specific properties, it is necessary to thoroughly understand the impact of mechanisms occurring at the level of the atomic or molecular structure and their impact on the macroscopic properties of materials. We expect that this knowledge will allow us to modify the macroscopic properties of materials (including elastic properties), to create new materials with improved properties, as well as materials with properties tailored to the needs of specific applications.

Understanding the impact of phenomena occurring at the microscopic level on the macroscopic properties of matter is a general issue that requires systematic basic research. To obtain this knowledge it means to examine the elastic properties of simplified models and show how they change as a result of modifications introduced at the structure level of these models. The hard sphere system (HSS) is one of the fundamental physical models that is widely used in the statistical mechanics of fluids and solids. In this model, intermolecular interactions are purely geometric in nature. They can be described using the so-called hard potential, which is equal to zero when the distance between the centres of any two spheres is not less than the sum of their radii (we say that the particles do not overlap) and infinite if this is not the case (then we say that the particles do overlap). The system of hard spheres is a well known reference model in fluid theory [1,2]. It is also the simplest model demonstrating the phase transition between a liquid and a crystal [1,3]. The answer to the question of what is the structure of the thermodynamically stable crystalline phase of hard spheres, is related to the hypothesis put forward by Johannes Kepler in 1611, that there is no denser packing of hard spheres than that which can be obtained by stacking the layers in which the spheres form a hexagonal pack [4]. In other words, Kepler supposed that it was impossible to pack hard spheres more densely than in the case of a densely packed face centered cubic structure (f.c.c.). This hypothesis has been proven by S. P. Ferguson and T. C. Hales at the end of the 20^th century and published at the beginning of this century [5]. Since the hexagonal layers mentioned by Kepler can be arranged not only in the same way as in f.c.c. structures and the densely packed hexagonal structure (h.c.p.) but also in many other ways (the number of which is infinite in the thermodynamic limit), the question arose which of these structures (which are equally dense in the close-packing limit) is thermodynamically stable? Numerical simulations showed that the structure of f.c.c. has a lower free energy than the h.c.p. structure. throughout the stability range of the crystalline phase [6,7,8,9]. Further simulations indicated that the free energy of the f.c.c. structure it is also lower than the free energies of other possible structures of densely packed hard spheres [10]. This leads to the conclusion that the thermodynamically stable crystalline phase of hard spheres has cubic symmetry and f.c.c. structure!

Computer simulations made it possible not only to determine the equation of state [11], but also the elastic properties of the system of hard spheres [12,13,14,15]. The determined elastic constants could be used to calculate Poisson's ratio (PR), which is the negative ratio of the relative change in transverse size to the relative change in longitudinal size, as the longitudinal stress changes. It turned out that PR, which for anisotropic systems usually depends on both the direction of change of the applied stress and the direction of strain measurement perpendicular to it, is negative when the stress change occurs in the direction [110] , and the strain is measured in the direction [110] [12,16]. It is worth noting at this point that the negativity of PR in the mentioned directions is found in systems with an f.c.c. [17] structure and most metals with cubic symmetry [18].

A negative Poisson's ratio is considered anomalous because it means that the body expands transversely to the direction of stretching, which is contrary to intuition based on observations of everyday life, e.g. a stretched rubber band shrinks in transverse directions. Materials exhibiting a negative Poisson's ratio, sometimes referred to as dilational materials [19], are usually called auxetics [20]. The first mechanical models showing NPR have been known for about 40 years [21,22,23]. The first reports of a thermodynamically stable and isotropic phase exhibiting this effect, date back to 1987 and concern the two-dimensional model of hard cyclic hexamers [24,25]. A rigorous analytical solution of this model, in the zero-temperature limit, was given in [26]. The first real material with a negative Poisson's ratio, a polyurethane foam, specially thermally treated under increased pressure, was created in 1987 by Lakes [27]. Since then, auxetics have been intensively studied, not only experimentally (e.g. [28,29,30]), but also by theoretical methods (e.g. [19,23,31,32,33]), and also using computer simulations (e.g. [15,34,35,36,37,38]).

Despite many years of research, the mechanisms of auxeticity at the microscopic level are still poorly explored, and we are far from fully understanding them. Computer simulations are an efficient tool for conducting systematic studies of selected microscopic models, which contribute to expanding our knowledge about the nature of auxetic properties.

Therefore, it is wise to start the research with the simplest models and then increase their complexity. Since cubic crystals show the highest symmetry among all periodic crystal structures, and the description of their elastic properties requires knowledge of only three independent quantities [39], it is natural to start research with microscopic models of this class of systems. The system of hard spheres is the simplest model of a solid with a face centred cubic structure. The research described below examined the influence of modifications introduced into the crystal structure of f.c.c. on the macroscopic elastic properties of simple models of hard particles.

In the study of the described models, computer simulations were used with the Monte Carlo method in an isothermal-isobaric ensemble, with a variable shape of the periodic box. The elastic properties of the studied systems were determined using the Parrinello-Rahman approach [40,41]. This well-established and improved at the Institute of Molecular Physics of the Polish Academy of Sciences, method allows for the determination of the elastic compliance tensor S_αβγδ directly from the fluctuations of the shape of the system. Knowledge of all tensor components allows for a complete description of the elastic properties of a crystal of any symmetry.

Modifications to the structure can be done in many ways. In the studies presented below, these modifications consisted of replacing some of the particles with particles of a different size. Such changes, involving the introduction of particles with diameters equal to σ', into the f.c.c. crystal of hard spheres with the diameters of σ, can be identified with introducing 'inclusions' into the system. The shape of the latter can be arbitrary. The inclusions used in the following studies had either cylindrical symmetry or constituted of a selected crystal plane. Visualizations of selected models with inclusions are presented in Fig. 1. Due to the fact that the models were considered in periodic boundary conditions, we are dealing with inclusions extending infinitely in one dimension (nanochannels) or two dimensions (nanolayers), respectively. Effectively, a system with a periodically arranged network of inclusions is created - a crystal containing a network of nanochannels or a stack of parallel nanolayers. This is schematically presented in Fig. 2, where exemplary models containing inclusions in the form of a nanochannel or nanolayer (Fig. 2a) are illustrated surrounded by their periodic images (Fig. 2b).

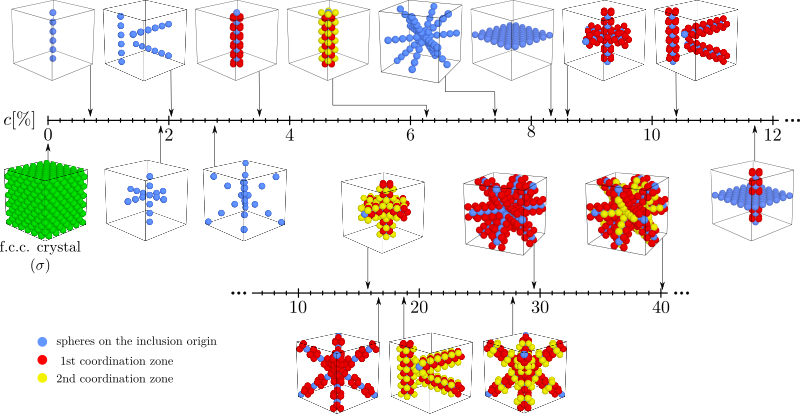
Figure 1. Selected models containing inclusions, arranged according to the size of the inclusions (the ratio of the number of spheres forming the inclusion to the number of all spheres in the system). The green σ particles have been removed from the remaining graphics, only to show the structure of the inclusions. All particles in other colours are the same and have a diameter of σ'. Different colours are used to show how far the particles are from the symmetry axis of the nanochannel or from the selected inclusion plane.

The simplest case of such modifications is the introduction into the supercell an inclusion in the form of a nanochannel, filled with hard spheres of a different size (oriented in the [001] direction - the so-called high symmetry direction, for which the Poisson ratio does not depend on the choice of the direction in the plane orthogonal to it). The size of the introduced nanochannel (the number of particles constituting an inclusion in relation to all particles in the system) can also be arbitrary. In the work [42], a nanochannel consisting of particles lying exactly on the selected crystal axis and their closest neighbors (one coordination zone) was used. For the selected pressure, it is shown that as a result of such a change, in each case when σ'≠σ the system loses cubic symmetry. It is shown that increasing the value of σ'> σ leads to tetragonal symmetry (422 symmetry class [43], described by six independent elastic compliance coefficients). At the same time, this causes the disappearance of auxetic properties (increase of Poisson's ratio from negative to positive values) towards [110][110]. It is worth noting that this is the direction in which a hard sphere crystal with f.c.c. symmetry shows auxetic properties. However, a decrease in the Poisson's ratio towards [111][112] was observed from the value of 0.065 to the value of −0.365, which shows that the inclusion used, allowed for the emergence of new directions in which auxetic properties occur. The lowest value of Poisson's ratio for this model was −0.87 when σ'/σ=1.09, which is a significant enhancement of the auxetic properties of the system compared to the f.c.c. crystal. homogeneous spheres, for which the smallest Poisson's ratio (in the direction of [110][110]) is ν∼−0.06. An important factor influencing the elastic properties of a system containing an inclusion is its size. In [44] the previous studies were expanded by simulations of systems containing periodic networks of nanochannels, oriented in the [001] direction, with fourteen different diameters. The narrowest nanochannel contained only 0.69% of the system's particles, and the largest as much as 56.25%. It was shown[44] that not only the size but also the shape of the inclusion used has a significant impact on the elastic properties of the system.

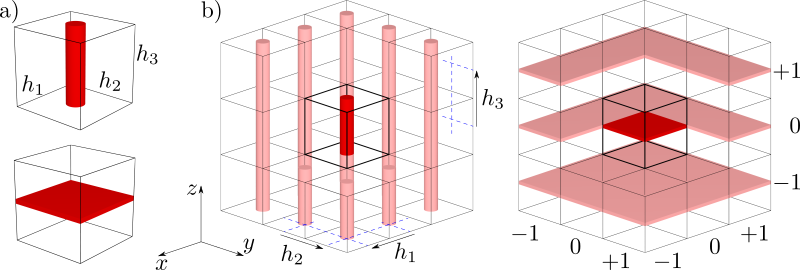
Figure 2.Example models with inclusions in the form of a nanochannel and nanolayer (a), presented in periodic boundary conditions (b). Some periodic images of both systems have been intentionally removed from the figure to improve readability.

The second simple system containing inclusions is the system (studied in [45]) whose supercell contains one layer of particles with a σ' diameter. This layer is oriented orthogonal to the [001] direction. We therefore obtain a system with a periodically arranged stack of (001) nanolayers. As the value of σ'/σ increases, the symmetry of the system changes from cubic to tetragonal (which is reflected in the form of the matrix of elastic compliance coefficients S. We observe an increase in the value of the (negative) Poisson's ratio towards [110][110] to zero. Unlike the system with a channel, the direction [111][112] does not become auxetic, however, we observe a decrease in the value of the (negative) Poisson's ratio in the direction [101][101] from the value of ν=−0.059 to the value of ν=−0.11 (at dimensionless pressure p^*=100). Therefore, we observe an increase in the auxeticity of the investigated model, compared to a monoatomic crystal with f.c.c. symmetry, but it is much smaller than the one observed in the system containing a nanochannel.

Since the inclusions in the investigated models can be shaped in any way, the logical consequence of the conducted research was to pose the question of how the elastic properties of the hard sphere system will change when we combine both types of inclusions in one model. The results, published in [46], showed that although we obtain a system of symmetry analogous to the previous two cases, its influence on the elastic properties of the model is completely opposite. Research carried out in three different thermodynamic conditions (different values of external, hydrostatic, pressure) showed that the combination of a nanochannel oriented in the [001] direction and a nanolayer placed orthogonally to it, completely eliminates the auxetic properties in the considered model. It has been observed that as the value of σ'/σ increases, the minimum Poisson's ratios measured in any of the directions increase, and we do not find any direction in the system for which the Poisson's ratio is negative. It has been shown that with the help of inclusions introduced into the crystal structure, it is possible not only to enhance auxeticity, but also to eliminate auxetic properties from the system.

In the works described above, the introduction of inclusions was associated with a change in the symmetry of the system from cubic to tetragonal (422 symmetry class). Therefore, the question was asked: would it be possible to design such inclusions that will not change the symmetry of the system, and what impact will they have on the elastic properties of the model? In [47,48] a system was considered in which a supercell consisting of N particles containing three nanochannels at the same time. They were oriented in the [100], [010] and [001] directions, respectively (orthogonal to each other). The three smallest sizes of nanochannels were examined: containing only particles lying on the inclusion axis[48] and covering their first and second coordination zones[47]. The proposed inclusions can be laid out in space in many ways. Two limiting cases were examined in which the symmetry axes of the nanochannels intersect each other or are separated by a certain number of lattice constants, greater than their diameters (no channel overlap). Research has shown that such a system of inclusions, from the point of view of elastic properties, behaves as if it had cubic symmetry, which is reflected in the values of the elastic compliance coefficients, that maintain (within the limit of computational accuracy) the equalities required by cubic symmetry, namely: S₁₁=S₂₂=S₃₃, S₄₄=S₅₅=S₆₆ and S₁₂=S₁₃=S₂₃, and the remaining elements of the matrix remain zero. These systems were tested for four different thermodynamic conditions. The results showed that, similarly to the model considered in [46], the introduction of three separated nanochannels also leads to the elimination of auxetic properties in the tested system. We have therefore obtained a system of 'cubic' symmetry without one of its inherent features, which is partial auxeticity. However, in the case of intersecting inclusions, the auxeticity was significantly reduced, but did not disappear. It has also been shown that the introduction of these inclusions usually leads to an increase in the anisotropy of the elastic properties of the crystal, however, in the case of one model (with separated nanochannels with a diameter encompassing only the first coordination zone of particles around the symmetry axis of the inclusions) it causes a strong decrease in the anisotropy of the elastic properties. For an isotropic system, the following equality holds: B₁₁−B₁₂=2B₄₄, where B_ij are the elements of the elastic constant matrix, which is the inverse of the elastic susceptibility matrix S. If this equation is expressed as the quotient of the left and right sides, it can be treated as the elastic anisotropy coefficient.

Another model with inclusions maintaining the symmetry of the f.c.c. crystal was a system whose supercell contained four nanochannels oriented along the four diagonals of the cube (direction [111] and its equivalents)[49]. It is shown that the anisotropy of the elastic properties of the system increases significantly, and the auxetic properties disappear with an increase in the value of σ'/σ (similarly to works [47,48]). Moreover, in the case of inclusions composed of wide nanochannels (with diameters covering two coordination zones around their symmetry axis), this effect is also visible when the σ'/σ value is less than 1. In systems in which inclusions covered a smaller percentage of the system's particles, such an effect was not observed. The current model, in which the largest of the examined inclusions included over 27% of particles in the system, shows that the concentration of inclusion particles (understood as the ratio of the number of particles forming the inclusion to the total number of particles) also has a significant impact on the change in the elastic properties of the tested models.

The last model considered so far, containing inclusions and maintaining cubic symmetry was the model containing six nanochannels oriented in the planes of the cube, in the [110] directions - and its symmetrical counterparts[50]. The tests were carried out for three different inclusion sizes and under four different thermodynamic conditions. The determined elastic properties for this model were compared with a model containing four nanochannels[49]. It has been shown that, contrary to the previous model, the auxetic properties decrease but do not disappear, what has been the case in a system containing four nanochannels. However, the research carried out in this work showed that the hardness and stiffness of the model with six channels not only does not decrease, compared to the pure crystal of hard spheres, but also increases significantly with the increase in the size of the particles forming the inclusion (σ'/σ). This is a completely new result that has not been observed in previously tested models.

It is also interesting how the elastic properties of hard systems with inclusions are influenced by the appearance of additional bonds between the particles. To check this, two cases were examined: a crystal composed of simple diatomic molecules (hard dimers) into which an inclusion was introduced in the form of a nanochannel filled with hard spheres[51], and a crystal of hard spheres with an analogous inclusion filled with dimers[52]. In the first case, the molecules forming the crystal were characterized by the lack of periodic translational ordering of the molecules, but the atoms of these molecules (in dense packing, when σ=1) formed a perfect f.c.c. network. Therefore, we are dealing here with the so-called degenerate crystal phase (DC) [53}. By introducing inclusions in the form of a nanochannel filled with spheres and oriented in the [001] direction into such a system, we obtain a kind of two-component composite. It is shown that when the value of σ'/σ increases, the negative Poisson's ratio in the [110] direction disappears, but at the same time the [111] direction becomes the direction in which we observe the appearance of auxetic properties (slightly larger than in case of a pure DC system. Moreover, it was shown that the composite resulting from the use of inclusions may exhibit elastic properties that go beyond the range of properties available for single-component systems composed separately from spheres or dimers.

The elastic properties of a hard sphere model with a channel in the [001] direction, filled with dimers[52], were compared with an analogous model composed only of hard spheres[42]. Two cases were examined: (i) in which the centres of the spheres constituting the dimer molecule were always located at a distance σ' from each other (regardless of the current value of σ'), and (ii) in which the centres of these spheres were from each other at a distance of σ'. In each of these cases, two sizes of nanochannels with diameters containing one or two particle coordination zones, respectively, were considered. Research has shown that the presence of molecules inside the inclusions has no effect on the Poisson's ratio, however, it can be seen that the presence of (a relatively small number of) molecules slightly increases the hardness and stiffness of the system.

Refereces

1. J. A. Barker, D. Henderson What is "liquid"? Understanding the states of matter Rev. Mod. Phys. 48: 587 (1976)
2. J. P. Hansen, I. R. McDonald Theory of Simple Liquids Academic Press, Amsterdam, The Netherlands, 2006
3. D. Frenkel, A. J. C. Ladd New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres J. Chem. Phys. 81: 3188-3193 (1984)
4. T. C. Hales Historical Overview of the Kepler Conjecture Discrete Comput. Geom. 36: 5-20 (2006) DOI: 10.1007/s00454-005-1210-2
5. T. C. Hales A proof of the Kepler conjecture Annals of Mathematics 162: 1065-1185 (2005) DOI: 10.4007/annals.2005.162.1065
6. L. V. Woodcock Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures Nature 385: 141-143 (1997)
7. L. V. Woodcock Entropy difference between crystal phases Nature 388: 236 (1997)
8. P. G. Bolhuis, D. Frenkel, S.-C. Mau, D. A. Huse Entropy difference between crystal phases Nature 388: 235-236 (1997)
9. K. V. Tretiakov, K. W. Wojciechowski Efficient Monte Carlo simulations using a shuffled nested Weyl sequence random number generator Phys. Rev. E 60: 7626-7628 (1999) DOI: 10.1103/PhysRevE.60.7626
10. S.-C. Mau, D. A. Huse Stacking entropy of hard-sphere crystals Phys. Rev. E 59: 4396 (1999)
11. W. G. Hoover, F. H. Ree Melting transition and communal entropy for hard spheres J. Chem. Phys. 49(8): 3609-3617 (1968) DOI: 10.1063/1.1670641
12. K. J. Runge, G. V. Chester Monte Carlo determination of the elastic constants of the hard-sphere solid Phys. Rev. A 36: 4852-4858 (1987)
13. D. Frenkel, A. J. C. Ladd Elastic constants of hard-sphere crystals Phys. Rev. Lett. 59(10): 1169 (1987})
14. S. Pronk, D. Frenkel Large difference in the elastic properties of fcc and hcp hard-sphere crystals Phys. Rev. Lett. 90: 255501 (2003) DOI: 10.1103/PhysRevLett.90.255501
15. K. V. Tretiakov, K. W. Wojciechowski Poisson's ratio of the fcc hard sphere crystal at high densities J. Chem. Phys. 123: 074509 (2005)
16. K. W. Wojciechowski Poisson's ratio of anisotropic systems Comp. Meth. Sci. Technol. 11: 73-79 (2005)
17. F. Milstein, K. Huang Existence of a negative Poisson ratio in fcc crystals Phys. Rev. B 19: 2030-2033 (1979) DOI: 10.1103/PhysRevB.19.2030
18. R. H. Baughman, J. M. Shacklette, A. A. Zakhidov, S. Stafstrom Negative Poisson's ratios as a common feature of cubic metals Nature 392: 362-365 (1998)
19. G. Milton Composite materials with Poisson's ratios close to -1 J. Mech. Phys. Solids 40(5): 1105-1137 (1992)
20. K. E. Evans Auxetic polymers: a new range of materials Endeavour 15: 170-174 (1991)
21. R. F. Almgren n isotropic three-dimensional structure with Poisson's ratio =-1 J. Elast. 15: 427-430 (1985)
22. A. G. Kolpakov Determination of the average characteristics of elastic frameworks J. Appl. Math. Mech. 49: 739-745 (1985)
23. J. N. Grima, K. E. Evans Auxetic behavior from rotating squares J. Mater. Sci. Lett. 19: 1563-1565 (2000) DOI: 10.1023/A:1006781224002
24. K. W. Wojciechowski Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers Mol. Phys. 61: 1247-1258 (1987)
25. K. W. Wojciechowski, A. C. Brańka Negative Poisson ratio in a two-dimensional isotropic solid Phys. Rev. A 40: 7222-7225 (1989)
26. K. W. Wojciechowski Two-dimensional isotropic model with a negative Poisson ratio Phys. Lett. A 137: 60-64 (1989)
27. R. S. Lakes Foam structures with a negative Poisson's ratio Science 235: 1038-1040 (1987)
28. B. D. Caddock, K. E. Evans Microporous materials with negative Poisson's ratios I. Microstructure and mechanical properties J. Phys. D-Appl. Phys. 22: 1877-1882 (1989)
29. S. Hirotsu Elastic anomaly near the critical point of volume phase transition in polymer gels Macromolecules 23: 905-907 (1990)
30. X. Xu, Q. Zhang, M. Hao, Y. Hu, Zh. Lin, L. Peng, T. Wang , X. Ren, C. Wang, Z. Zhao, Ch. Wan, H. Fei, L. Wang, J. Zhu, H. Sun, W. Chen, T. Du, B. Deng, G. J. Cheng, I. Shakir, Ch. Dames, T. S. Fisher, X. Zhang, H. Li, Y. Huang, X. Duan Double-negative-index ceramic aerogels for thermal superinsulation Science 363: 723-727 (2019) DOI: 10.1126/science.aav7304
31. L. Rothenburg, A. A. Berlin, R. J. Bathurst Microstructure of isotropic materials with negative Poisson's ratio Nature 354: 470-472 (1991)
32. H. Kimizuka, H. Kaburaki Mechanism for negative Poisson ratios over the α-β transition of cristobalite, SiO₂: A molecular-dynamics study Phys. Rev. Lett. 84(24): 5548-5551 (2000) DOI: 10.1103/PhysRevLett.84.5548
33. I. Shufrin, E. Pasternak, A. V. Dyskin Hybrid materials with negative Poisson's ratio inclusions Int. J. Eng. Sci. 89: 100-120 (2015)
34. Wm. G. Hoover, C. G. Hoover Searching for auxetics with DYNA3D and ParaDyn Phys. Status Solidi B-Basic Solid State Phys. 242(3): 585-594 (2005) DOI: 10.1002/pssb.200460377
35. K. V. Tretiakov, K. W. Wojciechowski Elastic Properties of Soft Sphere Crystal from Monte Carlo Simulations J. Phys. Chem. B 112: 1699-1705 (2008)
36. P. M. Piglowski, K. W. Wojciechowski, K. V. Tretiakov Partial auxeticity induced by nanoslits in the Yukawa crystal Phys. Status Solidi-Rapid Res. Lett. 10: 566-569 (2016) DOI: 10.1002/pssr.201600119
37. T. Shepherd, K. Winwood, P. Venkatraman, A. Alderson, T. Allen Validation of a Finite Element Modeling Process for Auxetic Structures under Impact Phys. Status Solidi B-Basic Solid State Phys. 257(10): 1900197 (2020) DOI: 10.1002/pssb.201900197
38. K. V. Tretiakov, P. M. Piglowski, K. W. Wojciechowski Auxeticity modifications and unit cell doubling in Yukawa fcc crystals with [001]-nanochannels filled by hard spheres Smart Mater. Struct. 32: 025008 (2023) DOI: 10.1088/1361-665X/acadbe
39. L. D. Landau, E. M. Lifshitz Theory of Elasticity Pergamon Press, London, UK 1986
40. M. Parrinello, A. Rahman Polymorphic transitions in single crystals: A new molecular dynamics method J. Appl. Phys. 52: 7182-7190 (1981)
41. M. Parrinello, A. Rahman Strain fluctuations and elastic constants J. Chem. Phys. 76: 2662-2666(1982)
42. J. W. Narojczyk, K. W. Wojciechowski, K. V. Tretiakov, J. Smardzewski, F. Scarpa, P. M. Pigłowski, M. Kowalik, A. R. Imre, M. Bilski, Auxetic properties of a f.c.c. crystal of hard spheres with an array of [001]-nanochannels filled by hard spheres of another diameter Physica Status Solidi B 256: 1800611 (2019) DOI: 10.1002/pssb.201800611
43. J. F. Nye Physical Properties of Crystalls, Their Representation by Tensors and Matrices Clarendon Press, Oxford, UK 1957
44. J. W. Narojczyk, K. V. Tretiakov, K. W. Wojciechowski, Partially auxetic properties of face-centered cubic hard-sphere crystals with nanochannels of different sizes, parallel to [001]-direction and filled by other hard spheres Physica Status Solidi B 259(6): 2200006 (2022) DOI: 10.1002/pssb.202200006
45. J. W. Narojczyk, K. W. Wojciechowski, Poisson's ratio of the f.c.c. hard sphere crystals with periodically stacked (001)-nanolayers of hard spheres of another diameter Materials 12: 700 (2019) DOI: 10.3390/ma12050700
46. J. W. Narojczyk, K. W. Wojciechowski, J. Smardzewski, A. R. Imre, J. N. Grima, M. Bilski, Cancellation of auxetic properties in f.c.c. hard sphere crystals by hybrid layer-channel nanoinclusions filled by hard spheres of another diameter Materials 14: 3008 (2021) DOI: 10.3390/ma14113008
47. J. W. Narojczyk, M. Bilski, J. N. Grima, P. Kedziora, D. Morozow, M. Rucki, K. W. Wojciechowski, Removing auxetic properties in f.c.c. hard sphere crystals by orthogonal nanochannels with hard spheres of another diameter Materials 15: 1134 (2022) DOI: 10.3390/ma15031134
48. J. W. Narojczyk, K. V. Tretiakov, K. W. Wojciechowski, Rise of the Poisson's ratio in f.c.c. hard sphere crystals with the narrowest orthogonal nanochannels filled by hard spheres of another diameter Computational Methods in Science and Technology 28(2): 61-75 (2022) DOI: 10.12921/cmst.2022.0000015
49. J. W. Narojczyk, K. V. Tretiakov, K. W. Wojciechowski, Poisson's ratio of f.c.c. hard-sphere crystals with cubic supercells containing four nanochannels filled by hard spheres of another diameter Physica Status Solidi B 259(12): 2200464 (2022) DOI: 10.1002/pssb.202200464
50. J. W. Narojczyk, K. V. Tretiakov, J. Smardzewski, K. W. Wojciechowski, Hardening of fcc hard sphere crystals by introducing nanochannels - auxetic aspects Physical Review E 108: 045003 (2023) DOI: 10.1103/PhysRevE.108.045003
51. J. W. Narojczyk, M. Kowalik, K. W. Wojciechowski Influence of nanochannels on Poisson's ratio of degenerate crystal of hard dimers, Physica Status Solidi B 253(7): pp.1324-1330 (2016) DOI: 10.1002/pssb.201600212
52. J. W. Narojczyk, The f.c.c. crystals of hard spheres with an array of [001]-nanochannel inclusions filled by the simplest hard sphere molecules Computational Methods in Science and Technology 29 (1–4): 37-44 (2023) DOI: 10.12921/cmst.2023.0000023
53. M. Kowalik, K. W. Wojciechowski Poisson's ratio of degenerate crystalline phases of three-dimensional hard dimers and hard cyclic trimers Phys. Status Solidi B-Basic Solid State Phys. 242: 626-631 (2005)